算法是为了解决实际问题的,问题简单,算法也简单;问题复杂,算法也相应复杂。为了便于交流和进行算法处理,往往需要将算法进行描述,即算法的表示。一般来说,算法可以采用自然语言表示、流程图表示、N-S图表示和伪代码表示。
1.自然语言表示
所谓自然语言,就是自然的随文化演化的语言,如英语、汉语等。通俗的讲,自然语言就是人们平时口头描述的语言。对于一些简单的算法,可以采用自然语言来口头描述算法的执行过程,如前面的统筹安排事件的例子。
但是随着需求的发展,很多算法都比较复杂,很难用自然语言描述,同时自然语言的表述繁琐难懂,不利于发展和交流。因此,需要采用其他的方法来进行表示。
其实,我国古代早起的算法也可以看作自然语言表示。正是为何我国古代算法起源早,但后来落后于西方国家的原因。
2.流程图表示
流程图是用一种图形表示算法流程的方法,其由一些图框和流程线组成。其中,图框表示各种操作的类型,图框中的说明文字和符号表示该操作的内容,流程线表示操作的先后次序。
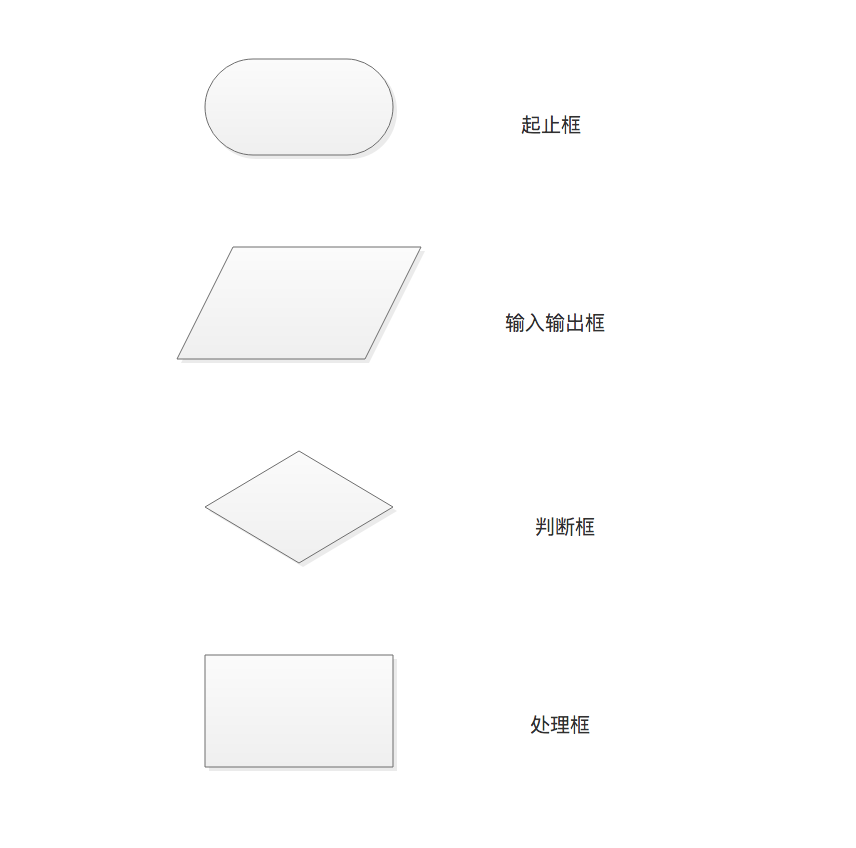
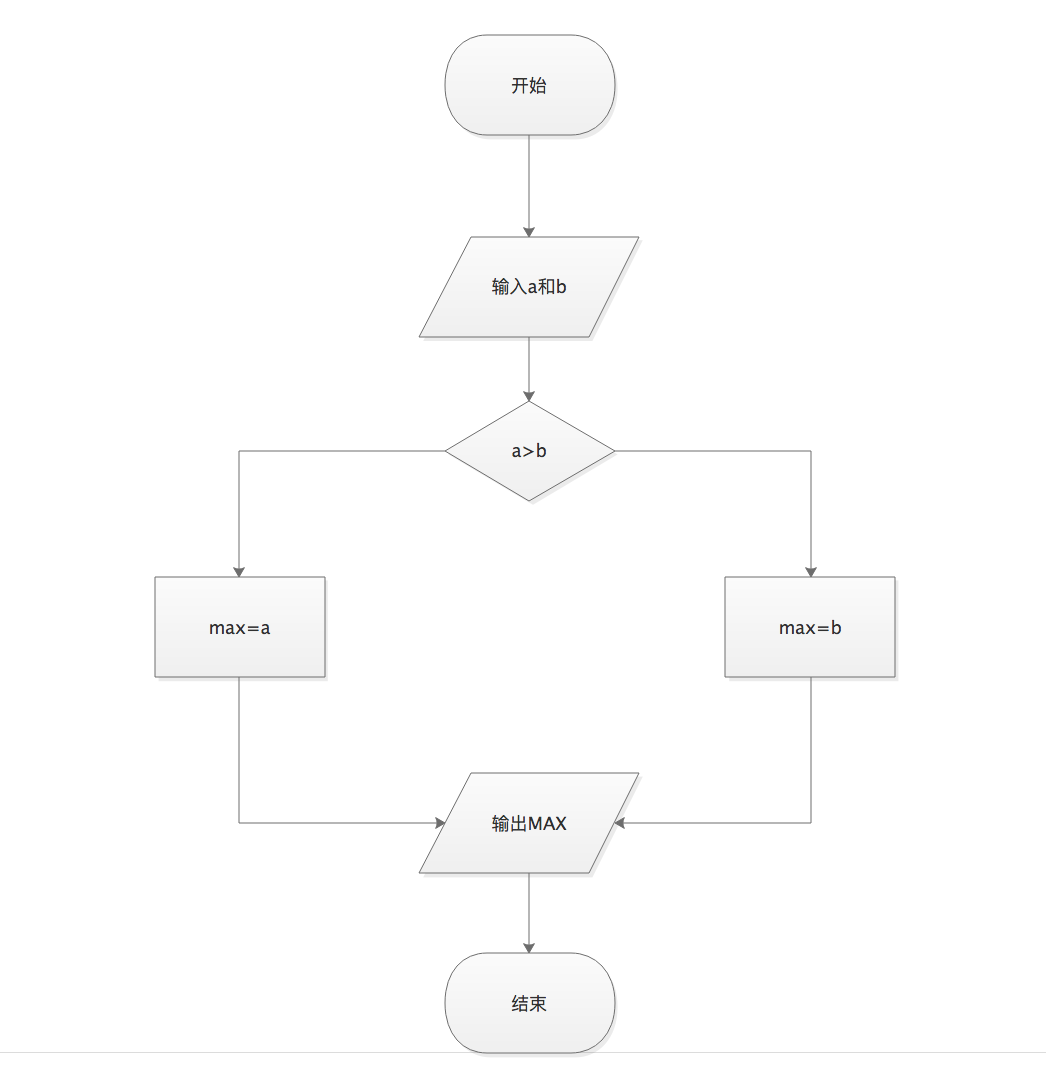
流程图最大的优点是简单直观,便于理解,在计算机算法领域有着广泛的应用。例如,计算两个输入数据a和b的最大值,可以采用如下图所示的流程图来表示。
在实际使用中,一般采用如下三种流程结构。
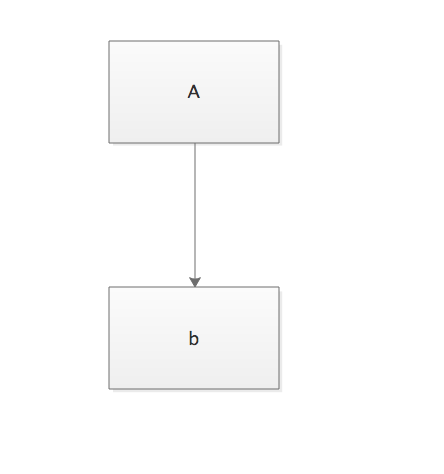
(1)顺序结构
顺序结构是最简单的一种流程结构,简单的一个接着一个的进行处理。一般来说,顺序结构适合于简单的算法。
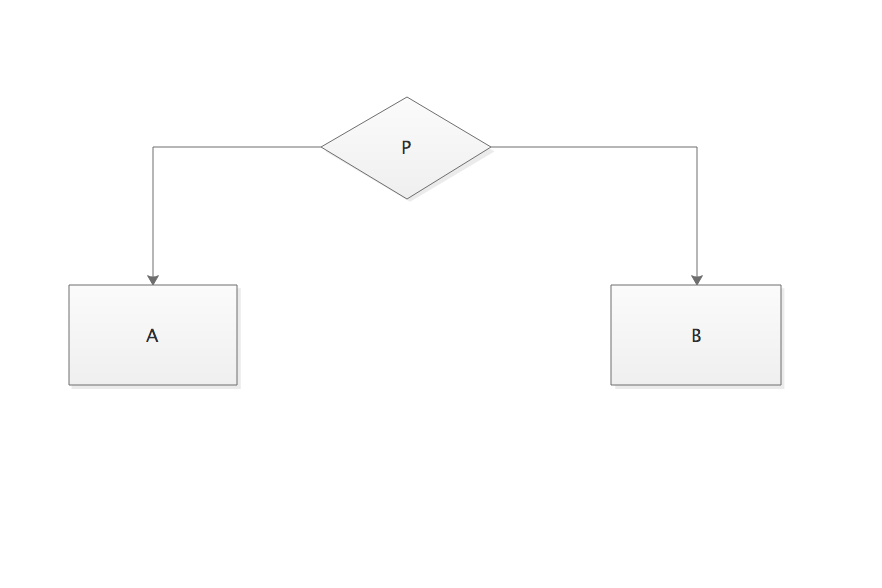
(2)分支结构
分支结构常用于根据某个条件来决定算法的走向。这里首先判断条件P,如果P成立,则执行B;否则执行A,然后再继续下面的算法。分支结构有时也称为条件结构。
(3)循环结构
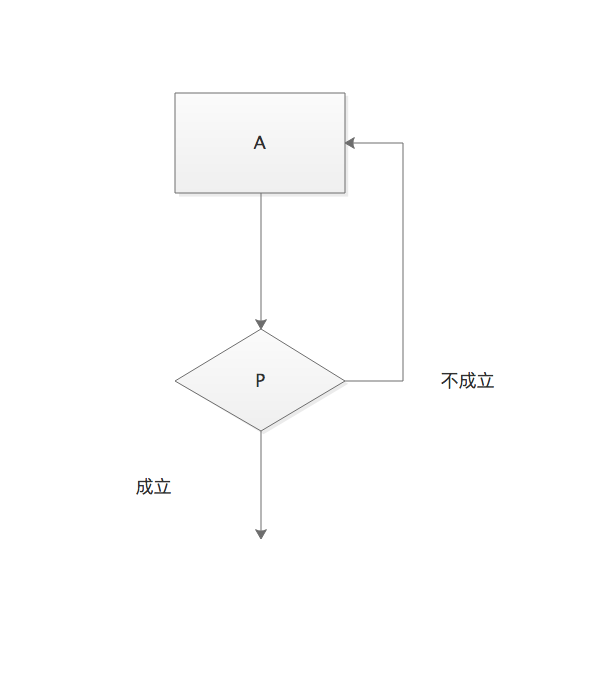
循环结构常用于需要反复执行的算法操作,按照循环的方式,可以分为当型循环结构和直到型结构
当型循环结构
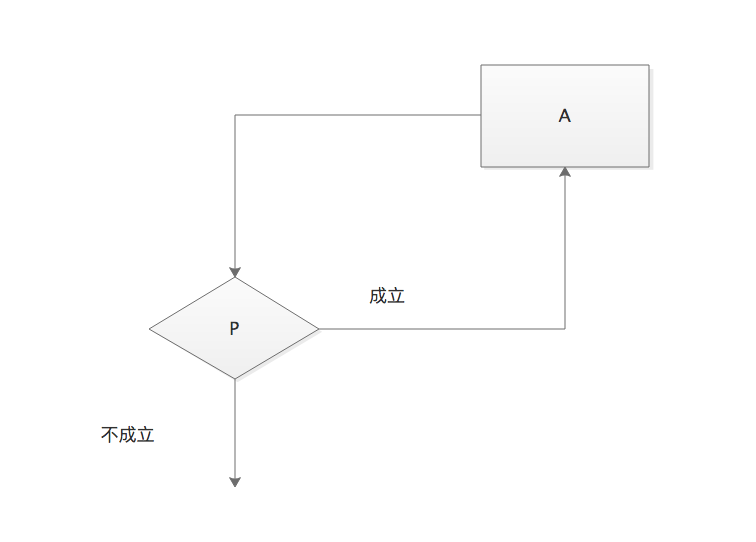
直到型循环结构
当型循环结构和直到型循环的区别如下:
当型循环结构先对条件进行判断,然后再执行,一般采用while语句来实现。
直到型循环结构先执行,然后再对条件进行判断,一般采用until、do…while实现。
3.N-S图表示
N-S图也称为盒图或者CHAPIN图,1973年由美国学者I.NASII和B.SHNEIDERMAN提出。他们发现采用流程图可以清楚的表示算法或程序的运行过程,但其中的流程线并不是必须的,因此创立了N-S图,在N-S图中,将整个程序写在一个大框图内,这个大框图由若干个小的基本框图构成。采用N-S图也可以方便的表示流程图的内容。
4.伪代码表示
伪代码(Pseudocode)是另外一种算法描述的方式。伪代码并非真正的程序代码,其介于自然语言和编程语言之间。因此,伪代码并不能在计算机中运行。使用伪代码的目的是将算法描述成一种类似于编程语言的形式,如C、C++、Java等。这样,程序员便可以很容易理解算法的结构,再根据编程语言的语法特点,稍加修改,即可实现一个真正的算法程序。
下面举一个简单的例子:
变量a<-输入数据
变量b<-输入数据
if a>b
变量max<-a
else
变量max<-b
输出变量max