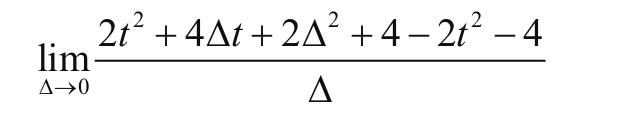BP神经网络的训练其实跟我们以前接触过的基于统计学的机器学习模型很相近,如果熟悉线性回归的朋友那就会觉得这个过程非常简单了.
我们先用线性回归的训练作为例子看一下这是一个什么过程
“机器学习”顾名思义就是机器通过观测到的事物进行归纳,进而总结出他们之间的规律,关系一类.在整个训练的过程中,我们倒要看看一个线性回归的模型究竟学到些什么,怎么学到的.作为铺垫,线性回归的训练过程如果能够看明白,那么下面再看这个两层神经网络也会非常清晰简单.
1.样本
一维线性回归可以说是机器学习中最简单的一种了,首先,我们会在一些场景中观察到很逗很多的数据对,例如,实验中小车在一个推力的作用下做加速运动,用手中的秒表和速度表,我们可以得到一些读数,形成下表这种观测记录:
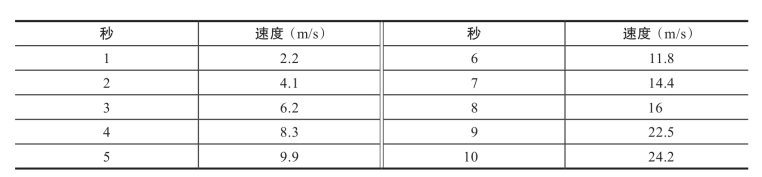
通过画图观察,我们发现横坐标代表的时间(s)和纵坐标代表的速度(m/s)有一种对应的关系,看上去像是线性关系–这个过程实在观察中进行的归纳和假设,至少看上去这两个数据确实给人这样的感觉
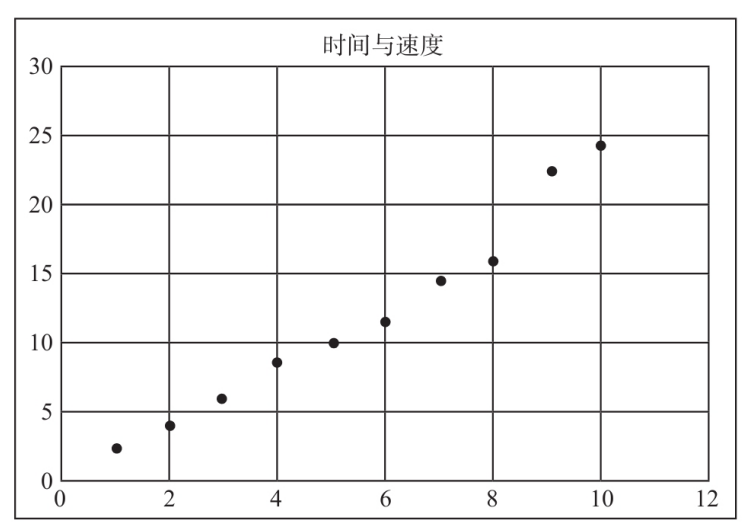
我们尝试画一条线从这一堆点中穿过去,会发现这条线基本上是可以满足或接近所有的点的,那么这条直线就是这些店的横纵坐标的关系描述–用(x,y)表示也可以.从数据科学的角度来看就是要解决的数据的量化和关系,而他们之间的量化表达式就是y=wx+b,这就是他们之间的关系
现在问题就变成了,我们通过一种方式把待定的系数w和b求出来就OK了.用什么原则来确定w和b的大小呢?毕竟计算机是不会像人那样去描点作图的,他只会做加减乘除和比大小,甚至乘除也是用加减来做的,减也是用加来做的,怎么办呢?其实方法是有的,我们先来看看一种叫”牛顿法”的东西
2.牛顿法
牛顿法从名字来看有点不知所云,不过说白了这是一种通过迭代来解方程的思路.虽然在神经网络和线性回归的训练中这个方法没办法直接使用,但是对于我们开阔思路还是大有好处的.
迭代的核心思路就是用步步逼近的方式来接近理论上的精确值,只要发现当前的试探值已经收敛到一个满足场景要求的误差精度就可以判断迭代结束,用这个试探值充当求解的目标值.这种方法可以使很多”直接法”无法求解的问题得到一个足够精确的近似解.例如,我们都知道一元二次方程y=ax²+bx+c通过配方和移项可以得到他的求根公式为:
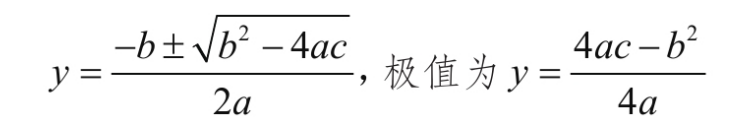
这种得到的以待定系数的函数作为表达式的解,就是我们说的解析解
迭代法与此不同,是通过多次”试探性”的计算并比对这个真实值之间的差距是否缩小来得到解.这种以有限成本的”优化”取代无限成本的”最优”的哲学思想是每一个工程人员都可以借鉴的思维方式.迭代法中有一个经典的方法,就是我们现在要说的牛顿迭代法(newton’s method),他是牛顿在18世纪提出的一种在实数域和复数域上近似求解方程的方法:
例如有一个一元方程:
f(x)=0
先不管f(x)具体的表达式是什么,或复杂或简单,假设f(x)=0真的有解,而r是满足f(x)=0的解,我们怎么找到这个r呢?要知道f(x)的表达式可能真的千奇百怪,还真不见得能通过人的手算,移项,配方…各种方法快速得到解.那就不妨用咱们刚刚说的这种迭代法的思路
设置一个初始值 x0,代入函数 y=f(x),则平面直接坐标系上会有点
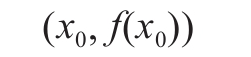
这个点落在曲线y=f(x)上
过点(x0,f(x0))做y=f(x)的切线L0,L0的方程就应该是:
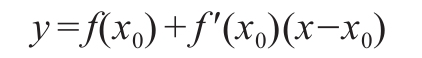
其中f'(x)就是f(x)的一阶导数
所谓导数,标准名称叫做导函数(derived function),这是高等数学中一个很基础而且很重要的概念,导数是一个函数而不是一个数字,以刚才的函数f(x)为例,贴着这个函数的曲线去做切线,在曲线上每一点所做的切线的斜率就是导函数在这一点的值,导函数用f'(x)来表示
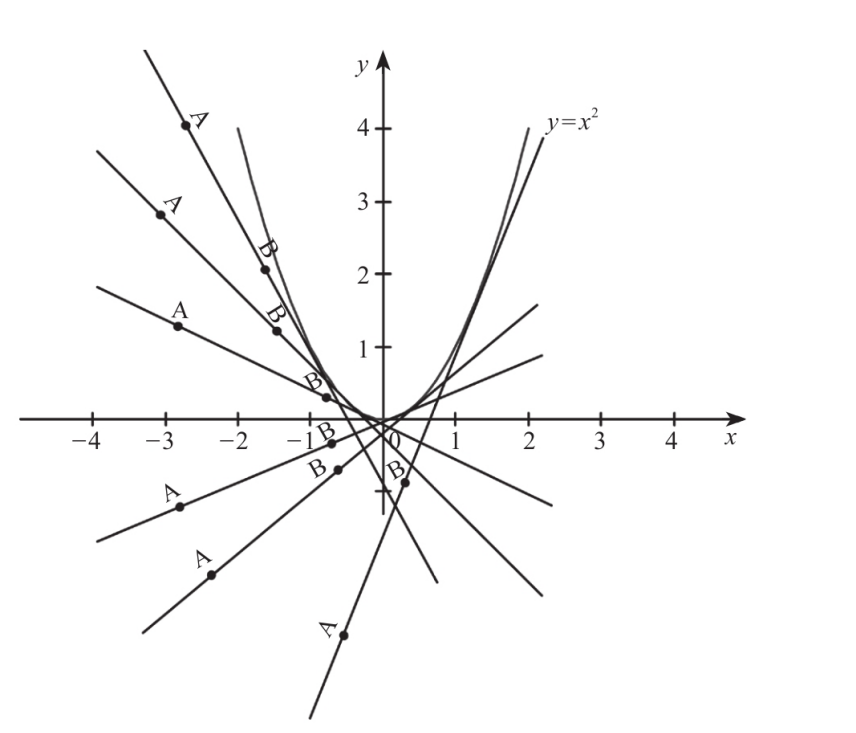
以y=x²为例,对图形上的每个点都做切线,都取切线斜率的话会得到一系列的x和斜率值,这新的对应关系x和斜率值就是我们刚刚说的f'(x)函数了.这同样一个函数,而输出值y的意义则表示原函数f(x)的斜率,有经验的朋友可能一下子就看出答案了y=x²这个函数的导函数是y=2x(见导函数)
回来看刚刚说过的方程y=f(x0)+f'(x0)(x-x0),如果你看不明白这个表达式是怎么出来的,那就做个代换,以我们最容易接受的y=kx+b的斜率与截距的方式来表示,那f'(x0)就是k.y=f(x0)+f'(x0)(x-x0)就可以改写为y=kx+(f(x0)-kx0),从图上看截距就是f(x0)-kx0
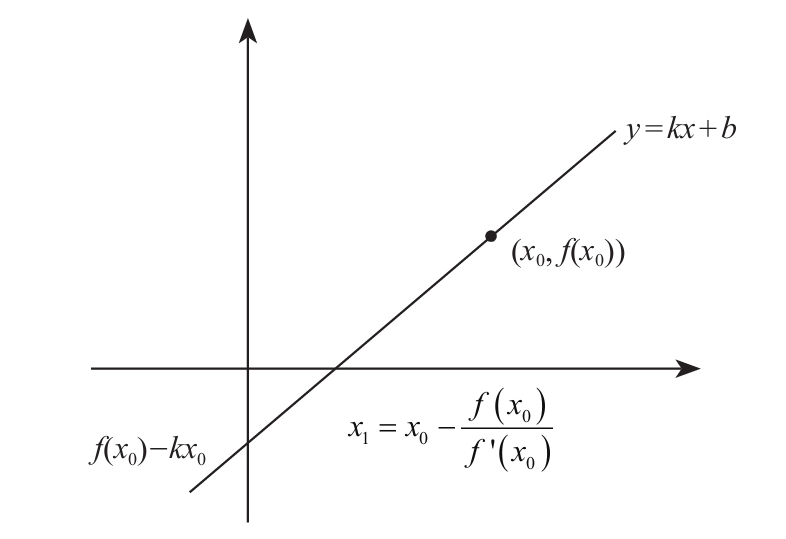
如果没问题的话,就继续耐心点往下看,这样就可以求出直线L0与X轴的交点的横坐标
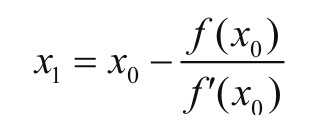
得到的x1为r的一次近似点
然后依葫芦画瓢,曲线y=f(x)上以相同方式过点(x1,f(x1))做y=f(x)的切线L1,得到L1与X轴的交点横坐标
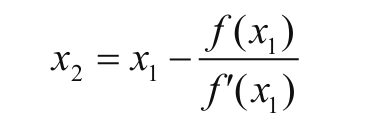
得到X2为r的二次近似点
以此种方式进行迭代,通项表达式为:
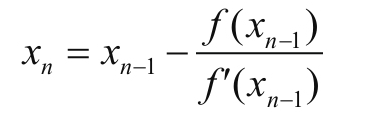
xn就称为r的n次近似点的值,这个公式就是牛顿迭代公式.整个迭代的收敛过程就像下图这样,通过n此的逼近最后得到r的近似值
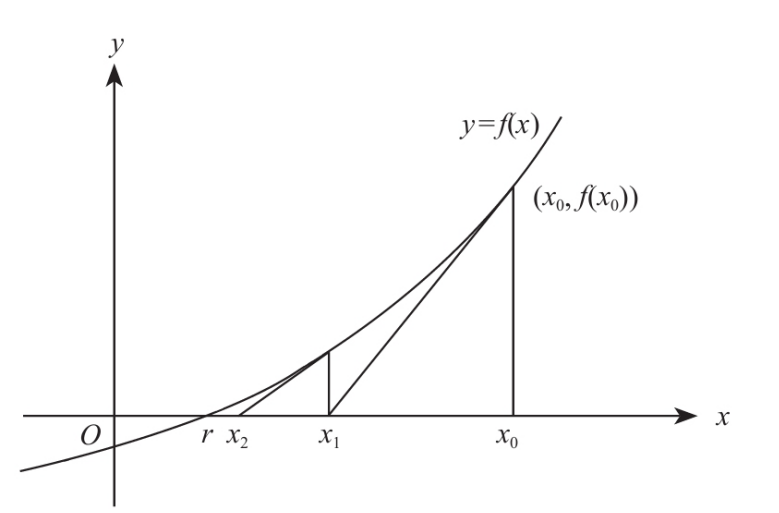
刚刚这种就是使用一次一次迭代来逼近最优解(局部最优解)的过程,而且牛顿迭代公式是可以推广到高维去使用的,比如二维,三维且各纬度可导的情况,不管导数多么复杂,这种方法都是通用的.
3.导数
既然说到导数这种东西我们就做个补充说明,这东西看上去确实让人感觉非常陌生,至少在日常生活中没有人会用这么一个数值文言词来交流,但是这种东西却是我们经常使用的,不行来看.我们平时说的速度–汽车的速度表上写着40km/h,就是一个导数的概念,我们来看看是怎么说的.
我们在初中物理课上早就学过这样的公式
S=VT
S是位移,V是速度,T是时间.这个公式的概念是我们按照速度V前进,例如一辆骑车每秒钟前进5米,当我行进了时间t之后.例如10秒,这时候我们会得到一个位移距离的大小,就是S.在刚刚这个例子我们很容易就能得出S=50米
但是,我们可别忘了,在这个公式中,s是可以用尺子量出来的,t是可以用秒表量出来的,这两种数据非常容易得到,但是你在初中课堂见过用什么直接去量速度吗?而恰恰相反,我们通常是使用:
V=S/T
来进行速度V的描述,用一段测量时间的T和其对应的位移S来定义其平均速度V,只要这个T不是0,刚刚这个公式就有意义
对于我们最为熟悉的均速直线运动来说,V在整个测量的过程中表现的非常理想–他不会变化,任意时刻V都是一个定值,所以S=VT肯定是不会有什么问题的.然而,如果在移动的过程中速度V是变化的,时快时慢,那在知道T的情况下S怎么求?还能按照刚刚的S=VT直接乘积求解吗?显然不能,那我们怎么做才更为科学合理呢?
我们知道速度V的定义本身就是指在一个瞬时状态下或者一段时间内的位移S与这段时间T的比值,我们更容易认知到且稳定的S和T定义了V
V=S/T
在均速运动的状态也不会看出有任何不妥的地方,只是我们刚才突然想到,如果V不是均速运动,而是在做变速运动,反正最后运动时间确实为t,总位移也确实为S,这种情况下
V=S/T
求出的V就是一个平均值了,而不是一个我们能够较好的,客观的描述真实瞬时V的值了–因为他每一刻可能都不一样,不是一个定值,这个时候我们可以很自然的萌生出一个想法,那就是,能不能试着用瞬时状态的位移S和瞬时状态的时间t来求出瞬时状态的V–也就是那一瞬间的速度大小,其实是可以的,这种定义其实就是我们用到的导数的定义.
那我们怎么来考虑某一刻的V呢?从原始的定义来看
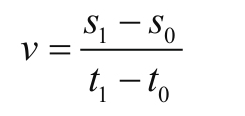
也就是说,在T0这一时刻,我们试着把这一刻的T0先记下来,并在同时记录位移S0的位置,然后在短短片刻之后,我们在T1时刻记录下这一刻的时间,并同时记录下S1,如果我们能够求得此时刻的
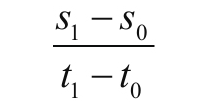
其实就是求得了此刻的V,你不用担心因为时间间隔太短会求出错误的值,比如求出一个0速度来,不会的,因为在S1-S0在减小的同时T1-T0也在减小,这个比值会趋于一个实数.
我们想想看,这种情况是不是当我手里有一个带有精确时间刻度的录像机就能轻松实现了?如果连每秒数百米速度的子弹都能扑捉的这么清楚的话,记录汽车的速度当然不在话下.

我们可以轻松得到一个S=S(T)的表达式,像图上所示这种可以精确到0.001秒的录像机在任何一个0.001分度的时刻都能记录下那一瞬间的时间和对应的位移了.假设我们一共录制了10秒的内容,那就从0秒开始到10秒把录像中位移位置的读数一个一个的画在EXCEL,至于录像机的时间分度是不是够小,区别如何,我们看看下面这几个图就能感觉出来了,对于一个加速度a=6m/s²的匀加速运动的物体来说,你会得到以下的图和对应的1秒以内的各种参数值
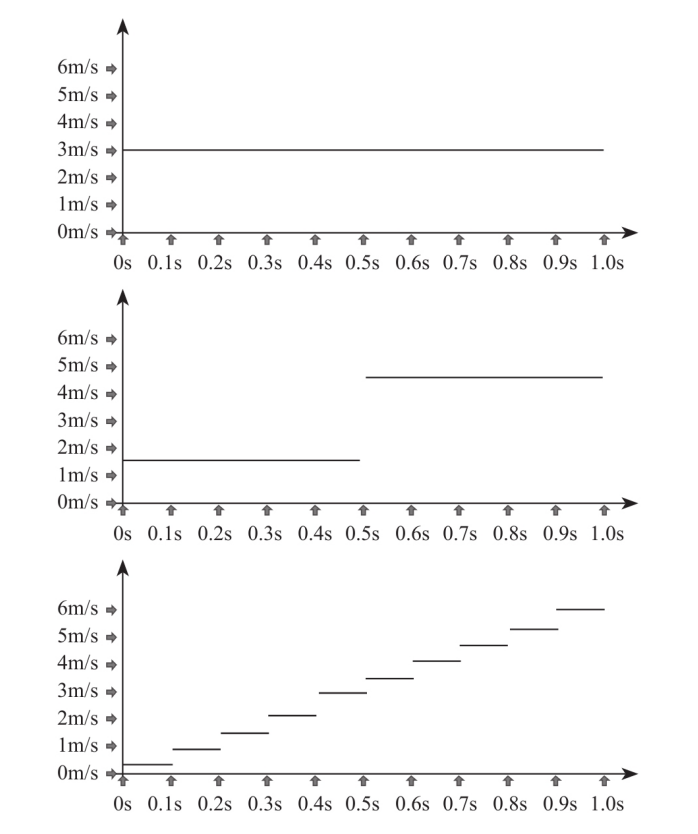
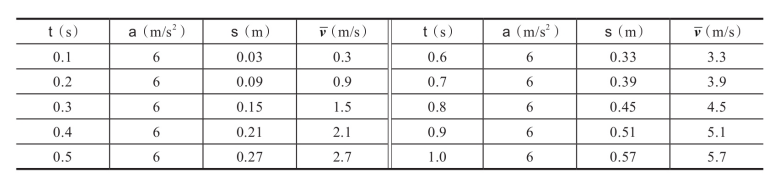
也就是说,从眼睛的感官上看,分度越大,曲线越不光滑,用两个临近点的位移S1-S0除以T1-T0也就越不精确,平均的意义越大,瞬时的意义越小.当然你可以再分,越分越平缓,越分越光滑,极限就是一条直线,只不过这条直线是一条斜率为6的直线而不再是最开始我们画出来的斜率为0的直线
在用高速摄像机录像所得到的S=S(T)这个函数中,速度的瞬时值为:
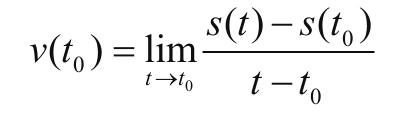
这里又出现一个表达式lim,读作limit,含义是极限.这个表示在某一瞬间T0.我们看这个公式非常眼熟,这不就是函数极限的公式么?没错,那下面精确与否几乎只取决于高速摄像机的时间分度了,因为从观测者的角度来看,在这个公式里,t只能取比T0大的最小的一个观测值,那也就是说,精度是0.1S的摄像机,那T-T0最小也只能求到0.1S的瞬时平均速度;精度是0.01S的摄像机,T-T0最小只能求到0.01S的瞬时速度…这个表达式会不会让你们误解
是摄像机购买时应该趋近高端机的过程?这里我们明确一个概念,那就是通过S(T)求解瞬时速度的思路.
如果还不是很清晰的话,那我们就来看一个例子,很快就会更为明确
如果有一个非均速运动的物体,他的运动位移可以表示为
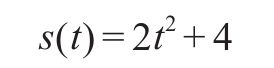
你可以认为就是通过录像机观察出来,最后用回归等方法归纳为这个公式的,那在T=5S时的瞬间速度是多大呢?那我们就求一下极限试试:
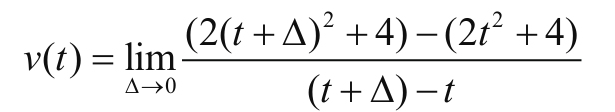
分子项有前后两个部分,前面的部分表示的是位移T时刻加上一个Δ时刻的总位移量,这个Δ读作delta,表示一个极小的偏移量.后面的部分表示的是在T时刻的位移量,两者的差表示任意T时刻后经过Δ这段时间的位移,也就是Δ时间的位移,而分母项Δ实际就是T+Δ与T的差值,这可以根据:
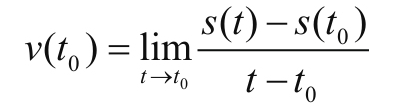
的定义得到.我们化简一下看: