激励函数(activation function)–也有翻译成激活函数的,也是神经元中的重要的组成部分.激励函数在一个神经元当中跟随在f(x)=wx+b函数之后,用来加入一些非线性因素.
sigmoid函数
sigmoid函数基本上是我们所有学习神经网络的人第一个接触到的激励函数,他的定义是这样的:
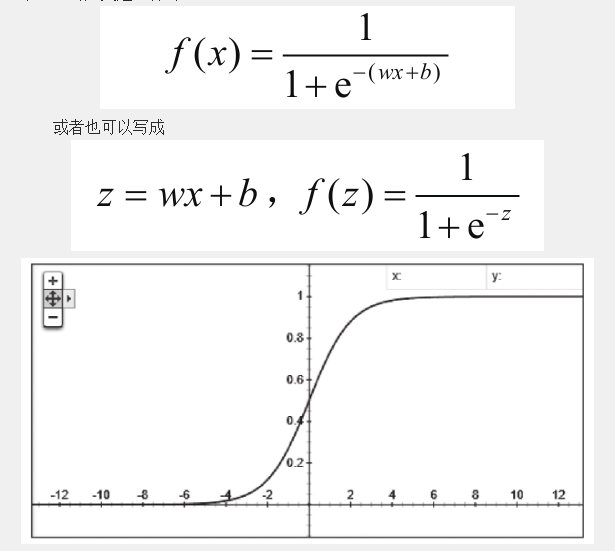
这里的横轴z,纵轴是f(z),在这个曲线中我们可以看到,对于一个高维的x向量的输入,wx两个矩阵做完内积之后,再加上b,这样的一个线性模型的结果充当自变量z再叠加到了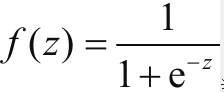 当中去.这就使得输入x与输出f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作的状态.
当中去.这就使得输入x与输出f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作的状态.
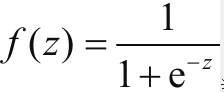 当中去.这就使得输入x与输出f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作的状态.
当中去.这就使得输入x与输出f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作的状态.这里的横轴是z,纵轴是f(z),在这个曲线中我们可以看到,对于一个高维的x向量的输入,在wx两个矩阵做完内积之后,再加上b,这样的一个线性模型的结果充当自变量z再叠加到了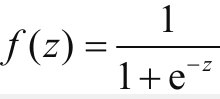 当中去.这就使得输入x和输出的f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作状态.当一个完整的神经元被定义的时候,他通常是带有线性模型和激励函数两个部分首尾相接而成的.所以最后一个神经元大概是这么个感觉,前半部分接收外界进来的x向量作为刺激,经过wx+b的线性模型后又经过一个激励函数,最后输出.这里只是为了看着方便,x只画了6条线,实际在工作中很多全连接网络里x要真画出来是要画几万条线不止的.
当中去.这就使得输入x和输出的f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作状态.当一个完整的神经元被定义的时候,他通常是带有线性模型和激励函数两个部分首尾相接而成的.所以最后一个神经元大概是这么个感觉,前半部分接收外界进来的x向量作为刺激,经过wx+b的线性模型后又经过一个激励函数,最后输出.这里只是为了看着方便,x只画了6条线,实际在工作中很多全连接网络里x要真画出来是要画几万条线不止的.
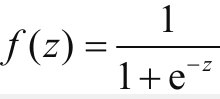 当中去.这就使得输入x和输出的f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作状态.当一个完整的神经元被定义的时候,他通常是带有线性模型和激励函数两个部分首尾相接而成的.所以最后一个神经元大概是这么个感觉,前半部分接收外界进来的x向量作为刺激,经过wx+b的线性模型后又经过一个激励函数,最后输出.这里只是为了看着方便,x只画了6条线,实际在工作中很多全连接网络里x要真画出来是要画几万条线不止的.
当中去.这就使得输入x和输出的f(x)关系与前面我们所举例的内容不同,前面我们只讲了f(x)以线性回归的方式去工作的过程,不过那不是他在神经网络中的工作状态.当一个完整的神经元被定义的时候,他通常是带有线性模型和激励函数两个部分首尾相接而成的.所以最后一个神经元大概是这么个感觉,前半部分接收外界进来的x向量作为刺激,经过wx+b的线性模型后又经过一个激励函数,最后输出.这里只是为了看着方便,x只画了6条线,实际在工作中很多全连接网络里x要真画出来是要画几万条线不止的.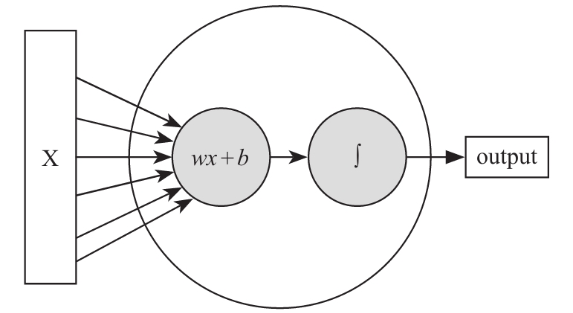
sigmoid函数是一种较早出现的激励函数,把激励值最终投射到了0和1两个值上.通过这种方式引入了非线性因素.其中1表示完全激活状态,0表示完全不激活的状态,其他输出值就介于两者之间,表示其激活程度不同.
说道为什么要引入非线性因素,这个可能是比较有趣的话题,因为最终用一个大的函数”网络”去拟合一个对应的关系的时候你会发现,如果仅有线性函数张的样子,那再怎么训练都不会有好结果.线性就是用形如f(x)=wx+b的表达式来表示的输入和输出的关系,而其他的都应该算作非线性关系了,后面我们会看到具体的例子.