我们如何面对的是离散的变量呢?比如,一个特征是否出现;是否是金色头发;就医者是否得病;

问题描述

线性回归的目标是基于一个连续的方程预测一个值,而本章的目标是预测一个样本属于某个确定类的概率.

本章中,我们将会使用一个基于一个连续方程预测一个值,而我们的目标是预测一个样本属于某个确定类的概率.

本章中,我们将会使用一个泛化的线性模型来解决回归问题.不同于之前的线性回归,我们这次的目标是解决一个分类问题,也就是将观察值贴上某个标签,或者是分入预先定义的类.

下图给我们展示了回归问题和分类问题的区别.第一幅图中,当输入x连续变化时,y也是连续变化的.

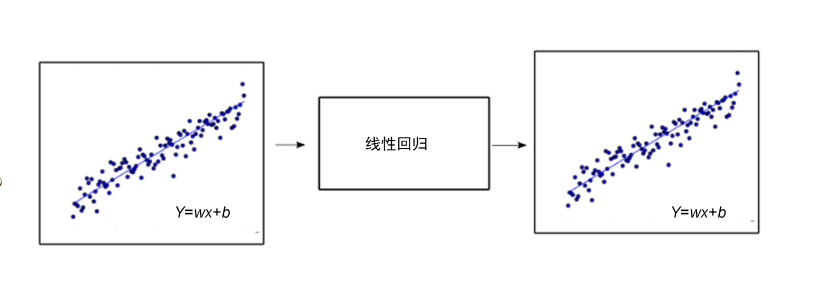
但是,在第二幅图中就不一样了,不管输入x怎么变化,y只有两种可能性.左边部分数据趋向于0,右边部分数据趋向于1

逻辑回归(logistic regression)的这个术语容易让人产生疑惑,明明要处理的是分类问题,为什么叫作回归?回归应该寻找一个连续值,而分类寻找的是离散值.

理解的关键就是,我们不仅仅是寻找一个表示类的离散值,我们还寻找属于该类可能性的连续值.

2.logistic函数的逆函数–logit函数

在我们开始学习logistic函数之前,我们先复习一个他的逆函数logit函数,logit函数和logistic函数息息相关,他们好多性质是关联在一起的.

logit函数的变量需要是一个概率p,更确切的说,需要是伯努利分布的事件概率.

(1)伯努利分布

伯努利分布又称为二项分布,也就是说他只能表示成功和失败两种情况.

1表示成功,概率p

0表示失败,概率q=1-p

一个服从伯努利分布的随机变量,其概率函数可以被表述为:

Pr(X=1)=1-Pr(X=0)=1-q=p

什么样的情况可以用伯努利分布来表示呢?当我们只有两种选择的时候(特征是否存在,事件是否发生,现象是否具有因果性,等等)

(2)联系函数

在我们建立广义线性模型之前,我们先要从线性函数开始,从独立变量映射到一个概率分布.

既然操作的是二值选项,我们自然会选择刚刚提到的伯努利分布,而连接函数这是对数几率函数.

(3)logit函数

我们能够使用一个函数,就是对发生率取对数,该函数被称作logit函数:

logit(p)=log(p/1-p)

这里面的(p/1-p)被称为事件的发生率,对其取对数,所以称为对数几率函数,简称对数函数,标记为logit函数.

由下图我们可以看到,该函数实现了从区间[0,1]到区间(-无穷,+无穷)之间的映射,那么我们只要将y用一个输入的线性函数替换,那么就实现了输入的线性变化和区间[0,1]之间的映射.

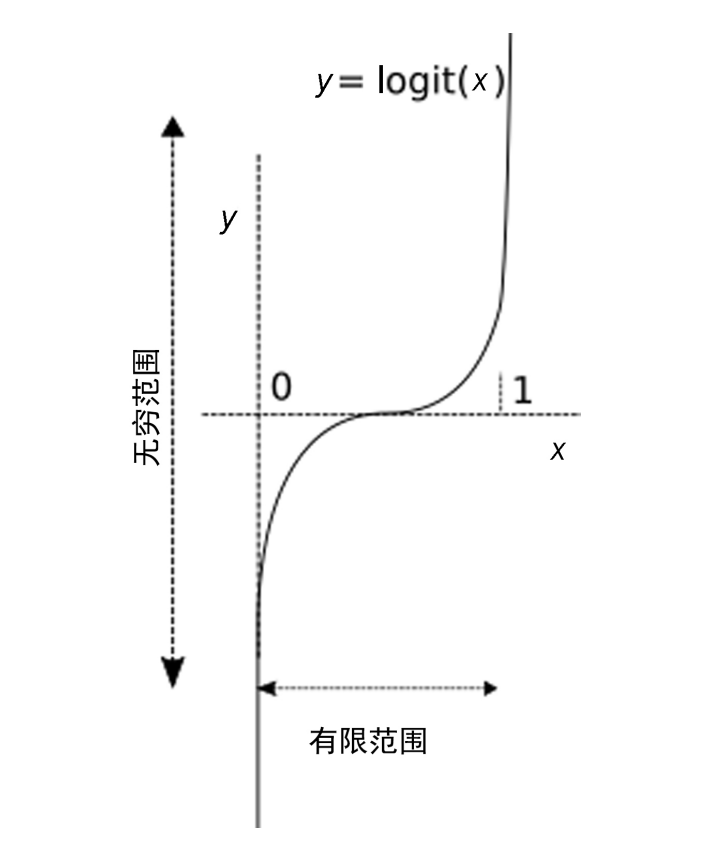
(4)对数几率函数的逆函数–logistic函数

我们计算一下对数几率的逆函数

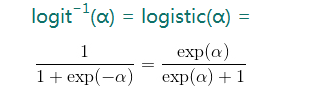
这是一个sigmoid函数

logistic函数将使得我们能够在我们的回归任务表示为二项选择

sigmoid函数的图形表示如下图所示

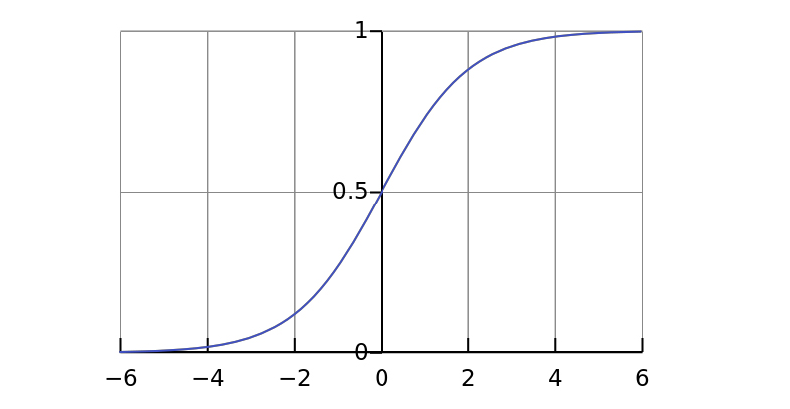
1))logistic函数做为线性模型的泛化

logistic函数定义如下:

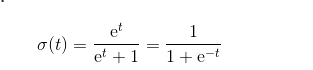
一般的解释就是t为一个独立变量,该函数将t映射到区间[0,1]之间,但是我们提升了这个模型,将t转变为变量x的一个线性映射(当x是一个多变量的向量时,t就是该向量中各个元素的线性组合)

我们可以将t表示为: t=wx+b

我们就能够得到以下方程:

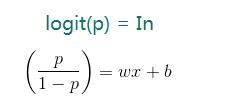
对于所有的元素,我们计算了回归方程,得出如下概率:

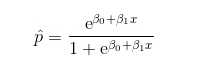
下图展示了任意范围的变量是如何映射到区间[0,1]的,而[0,1]之间的数,就可以被表示为一个时间发生的可能性.

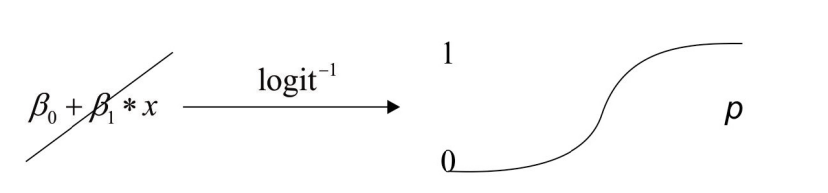
线性函数的参数起什么作用呢?他们可以改变直接的斜率和sigmoid函数零的位置,通过调整线性方程中的参数,可以用来缩小预测值与真实值之间的差距.

2))logistic函数的属性

函数空间中每个曲线都可以被描述成他说应用的可能目标.具体到logistic函数:

事件的可能性p依赖于一个或者多个变量,比如,根据之前的资历,预测获奖的可能性.

对于特定 的观察,估算事件发生的可能性.

预测改变独立变量对二项相应的影响

通过计算可能性,将观测分配到某个确定的分类

3))损失函数

前面的章节中,我们学习了近似的函数,他能够得到样本属于某个确定类的可能性,为了计算预测与正式结果的切合程度,我们需要仔细选择损失函数.

损失函数可以表达为:

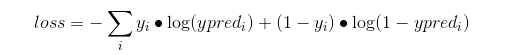
该损失函数的主要性质就是偏爱相似行为,当误差超过0.5的时候,惩罚会急剧增加.

(5)多类分类应用–softmax回归

到现在为止,我们只是对二类分类进行处理,能够得到发生或者不发生的概率p

当我们面对多于二类的情况,通常有两种方法:一对多和一对所有

第一类技术计算多个模型,针对每个类都计算一个1对所有的概率

第二类技术只计算出一个概率集合,每个概率表示属于其中某一类的可能性

第二类技术的输出是softmax回归格式,这是logistic回归对于n类的泛化

于是我们就要对我们的训练样本做出改变,从二值标签(),到向量标签().其中K是类的数目,y可以取k个不同的值,而不限于2.

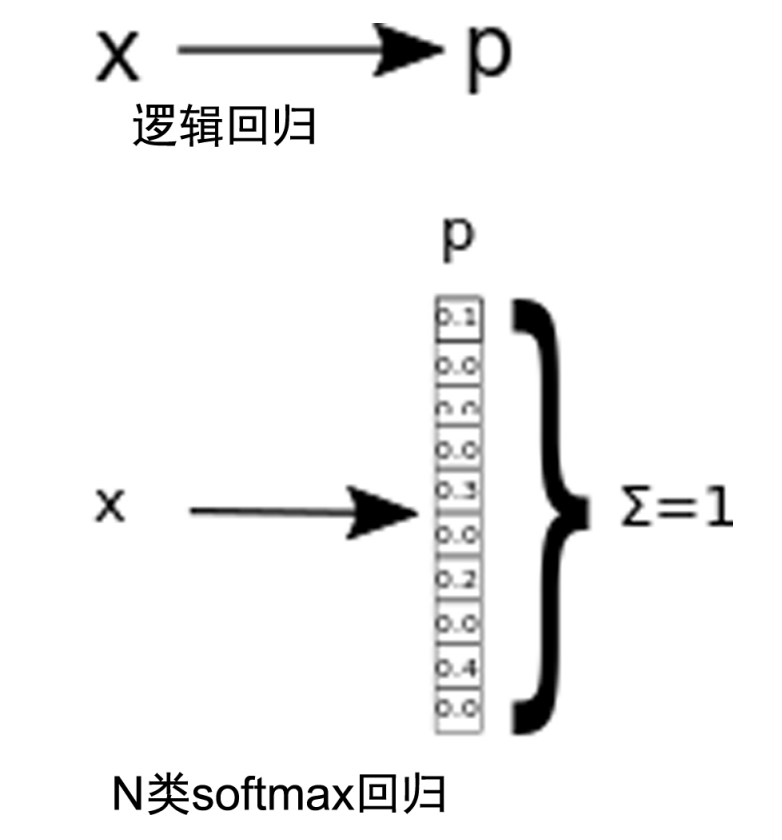
对于这个技术,我们针对每个测试输出x,估算出P(y=k|x),其中k=1,1,k.softmax回归的输出将会是一个k维的向量,每个数值对应的是该属于当前类的概率

如下图所示,我们表示了由输入到逻辑回归发生率p的映射

1))损失函数

softmax的损失函数是一种改动的交叉熵函数,也是非线性的,惩罚混乱度高的情况,偏爱混乱度低的情况.

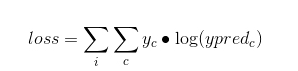
这里,c是类的索引,i是训练样本的索引,当yc为1表示当前样品属于类x

展开该表达式,我们能够得到:

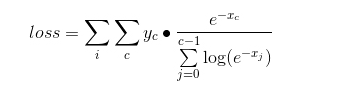
2))为迭代方法进行数据正则化

正如我们之前的部分所看到的,逻辑回归使用梯度下降方法来最小化损失函数,下图为数据正则化

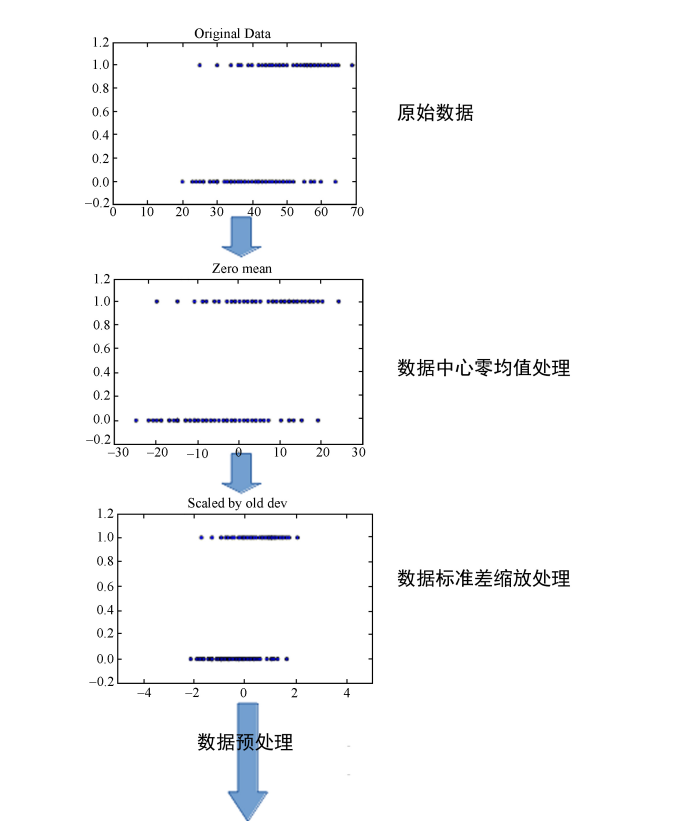
该方法对特征数据的分布和形式敏感.

正是这个原因,我们要先对数据进行预处理,以期待获得更好,更快的收敛结果.

我们不去考虑正则化的理论解释.直觉地来看,数据正则化的时候,相当于平滑误差表面,使得梯度下降迭代更快的收敛到最小误差.

3))一位有效输出表示

为了能让softmax作为回归函数的损失函数,我们必须使用一种编码类型,叫做一位有效(one hot)这种编码方式把一个表示类的数据,转变为一个阵列,而原来表示类的数值列表,经过编码后将称为阵列列表,阵列的长度是列表中最大数值的数目,对应的该类的数目加1的那个元素被至为1,其他元素都是0