Statsmodels是用于探索数据、估计模型,并运行统计检验的Python包。在这里,让我们使用它来构建一个简单的线性回归模型,为setosa类中花萼长度和花萼宽度之间的关系进行建模。
首先,通过散点图来目测这两者的关系。
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib.font_manager import *
#定义自定义字体
myfont = FontProperties(fname='/temp/msyh.ttf')
df = pd.read_csv("/temp/iris.data",names=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度', '类别'])
fig, ax = plt.subplots(figsize=(7,7))
ax.scatter(df['花萼宽度'][:50], df['花萼长度'][:50])
ax.set_ylabel(u'花萼长度',fontproperties=myfont)
ax.set_xlabel(u'花萼宽度',fontproperties=myfont)
ax.set_title(u'花萼长度 花萼宽度', fontproperties=myfont,fontsize=14, y=1.02)
plt.show()
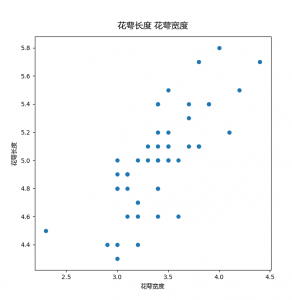
我们可以看到,似乎有一个正向的线性关系,也就是说,随着花萼宽度的增加,花萼长度也会增加。接下来我们使用statsmodels,在这个数据集上运行一个线性回归模型,来预估这种关系的强度。
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
from matplotlib.font_manager import *
#定义自定义字体
myfont = FontProperties(fname='/temp/msyh.ttf')
df = pd.read_csv("/temp/iris.data",names=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度', '类别'])
y = df['花萼长度'][:50]
x = df['花萼宽度'][:50]
X = sm.add_constant(x)
results = sm.OLS(y, X).fit()
print(results.summary())
输出
OLS Regression Results
==============================================================================
Dep. Variable: 花萼长度 R-squared: 0.558
Model: OLS Adj. R-squared: 0.548
Method: Least Squares F-statistic: 60.52
Date: Fri, 08 Sep 2017 Prob (F-statistic): 4.75e-10
Time: 17:21:06 Log-Likelihood: 2.0879
No. Observations: 50 AIC: -0.1759
Df Residuals: 48 BIC: 3.648
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.6447 0.305 8.660 0.000 2.031 3.259
花萼宽度 0.6909 0.089 7.779 0.000 0.512 0.869
==============================================================================
Omnibus: 0.252 Durbin-Watson: 2.517
Prob(Omnibus): 0.882 Jarque-Bera (JB): 0.436
Skew: -0.110 Prob(JB): 0.804
Kurtosis: 2.599 Cond. No. 34.0
==============================================================================
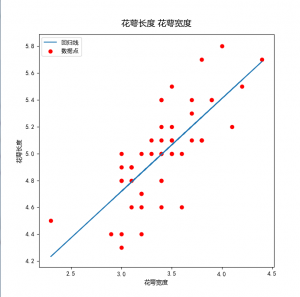
由于这是一个线性回归,该模型的格式为Y = Β0+Β1X,其中B0为截距而B1是回归系数。在这里,最终公式是花萼长度 = 2.6447 + 0.6909 × 花萼宽度。
我们也可以看到,该模型的R2值是一个可以接受的0.558,而p值 (Prob)是非常显著的——至少对于这个类而言。
获取从模型所得的回归线。
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
from matplotlib.font_manager import *
from pylab import *
#定义自定义字体
myfont = FontProperties(fname='/temp/msyh.ttf')
#解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus']=False
mpl.rcParams['font.sans-serif'] = ['SimHei']
df = pd.read_csv("/temp/iris.data",names=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度', '类别'])
y = df['花萼长度'][:50]
x = df['花萼宽度'][:50]
X = sm.add_constant(x)
results = sm.OLS(y, X).fit()
fig, ax = plt.subplots(figsize=(7,7))
ax.plot(x, results.fittedvalues, label=u'回归线')
ax.scatter(x, y, label=u'数据点', color='r')
ax.set_ylabel('花萼长度',fontproperties=myfont)
ax.set_xlabel('花萼宽度',fontproperties=myfont)
ax.set_title('花萼长度 花萼宽度', fontproperties=myfont,fontsize=14, y=1.02)
ax.legend(loc=2)
plt.show()