冒泡排序
package day0505;
import java.util.Arrays;
import java.util.Random;
public class Test1 {
public static void main(String[] args) {
int[] arr = rand();
System.out.println(Arrays.toString(arr));
int[] result = sort(arr);
System.out.println(Arrays.toString(result));
}
private static int[] sort(int[] arr) {
for (int n = 0; n < arr.length - 1; n++) {
for (int i = arr.length - 1; i > n; i--) {
boolean flag = false;
int temp;
if (arr[i] < arr[i - 1]) {
flag = true;
temp = arr[i - 1];
arr[i - 1] = arr[i];
arr[i] = temp;
}
if (!flag) break;
}
}
return arr;
}
private static int[] rand() {
int n = new Random().nextInt(6) + 5;
int[] arr = new int[n];
for (int i = 0; i < arr.length; i++) {
arr[i] = new Random().nextInt(100);
}
return arr;
}
}
数组工具类 Java.util.arrays
Arrays.toString
把数组连接成字符串
Arrays.Sort(数组)
对数组进行排序
基本类型数组:优化的快速排序算法
引用类型数组:优化的合并排序算法
Arrays.copyOf(数组,新的长度)
对数组进行赋值
Arrays.Fill(数组,值)
用新值覆盖数组原值
数组的复制
Arrays.copyOf()
System.Arraycopy(
原数组,原数组起始位置,目标数组,目标数组起始位置,复制数据量
)
二维数组
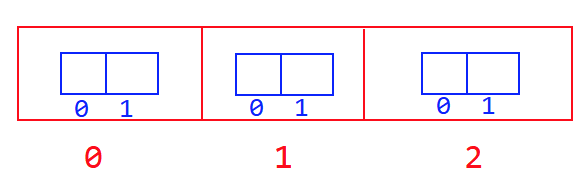
创建二维数组
int[][] a = new int[3][2];
新建一个外围数组长度 3
新建三个内部数组,长度都是2
内部数组存默认值0
外数组存内存地址
int[][] a = new int[3][];
只创建一个外围数组,长度3
外围数组中存默认值 null(空)
之后可以再新建数组,放入外围数组
a[0] = new int[3];
a[1] = new int[]{5,3,2,6,4};
a[2] = new int[]{2,4,1,6};
n int[][] a = {
{6,3,7},
{3,8,5,3,8},
{2,7,9,4}
};
方法的递归
在方法中调用自身
f() {f();}
一步一步地简化问题,简化成最简问题,再反向倒推求出结果
一般不同时做多次递归调用,否则运算量会急剧增加
可以考虑用循环代替
阶乘
package day0507;
import java.util.Scanner;
public class Test1 {
public static void main(String[] args) {
System.out.print("输入一个整数:");
int i = new Scanner(System.in).nextInt();
long result = f(i);
System.out.println(result);
}
private static long f(int i) {
if (i == 1) return 1;
return i * f(i - 1);
}
}
斐波那契数
1 1 2 3 5
package day0508;
import java.util.Scanner;
public class Test1 {
public static void main(String[] args) {
System.out.print("第几个斐波那契数:");
int i = new Scanner(System.in).nextInt();
long result = f1(i);
System.out.println(result);
}
private static long f1(int i) {
long a = 1;
long b = 1;
for (int n = 3; n <= i; n++) {
b = a + b;
a = b - a;
}
return b;
}
private static long f(int i) {
if (i <= 2) return 1;
return f(i - 2) + f(i - 1);
}
}