1.从数据中学习–无监督学习

无监督学习可以从给定的数据集中找到感兴趣的模式(parrern),无监督学习,一般不给出模式的相关信息.所以,无监督学习算法需要自动探索信息是怎么组成的,并识别数据中的不同结构.

2.聚类的概念

对于没有标签(unlabeled)的数据,我们首先能做的,就是寻找具有相同特征的数据,将他们分配到相同的组.

为此,数据集可以分成任意数量的段(segment),其中每个段都可以用他的成员的质量中心(质心,centroid)来替代表示.

为了将不同成员分配到相同的组中,我们需要定义一下,怎样表示不同元素之间的距离(distance),在定义距离之后,我们可以说,相对于其他质心,每个类成员都更靠近自己所在类的质心.

典型的聚类算法的结果和聚类中心的表示

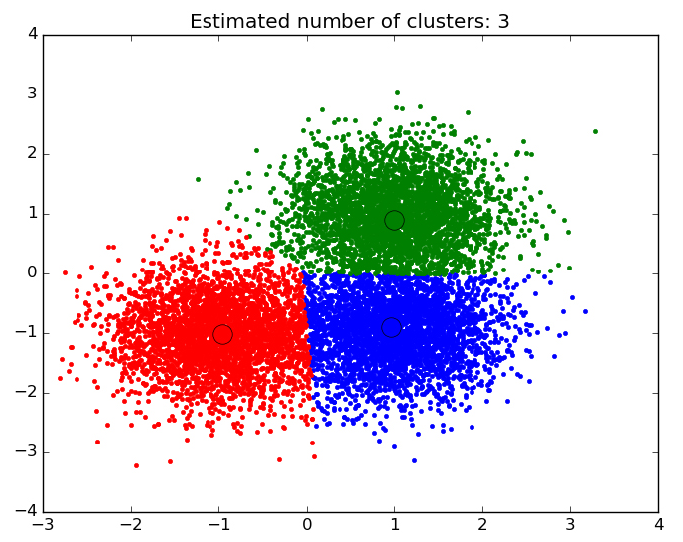
3.k均值

k均值(k-means)是一种常见的聚类算法,并且比较容易实现.它非常直接,一般是用于分析数据的第一步,经过该处理,我们能够得到一些关于数据集的先验知识.

(1)k均值的机制

k均值算法试图将给定的数据分割为k个不相交的组(group)或簇(cluster),每个簇的指标就是该组所有成员的均值,这个点通常称为质心,指具有相同名称的算术实体,并且可以被表示为任意纬度中的向量.

k均值是一个朴素的方法,因为它在不知道簇的数量的前提下,寻找合适的质心.

要想知道多少个簇能够比较好的表示给定数据,一个常用的方式是Elbow方法.

(2)算法迭代判据

此方法的判据和目标是最小化簇成员到包含该成员的簇的实际质心的平方距离的总和.这也称为惯性最小化,k均值的损失函数如下:

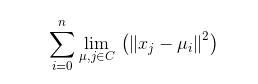
(3)k均值算法拆解

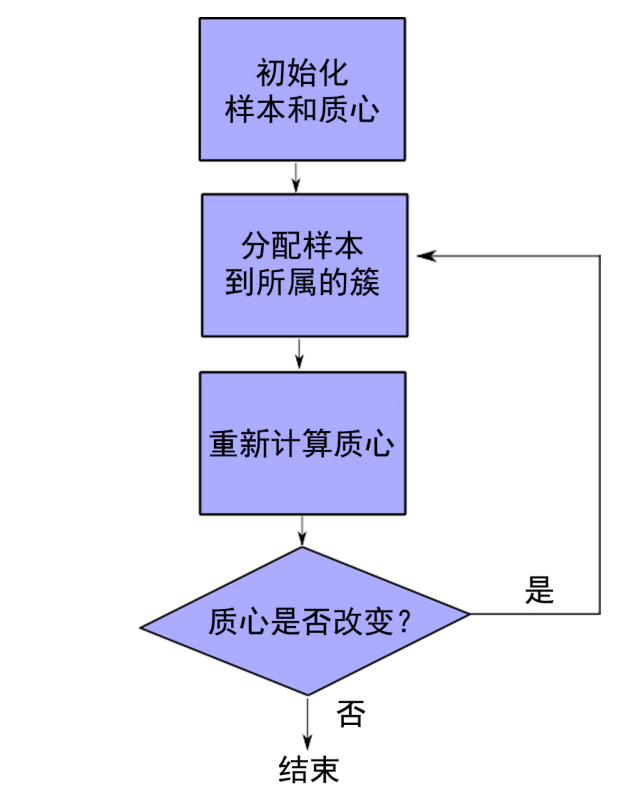
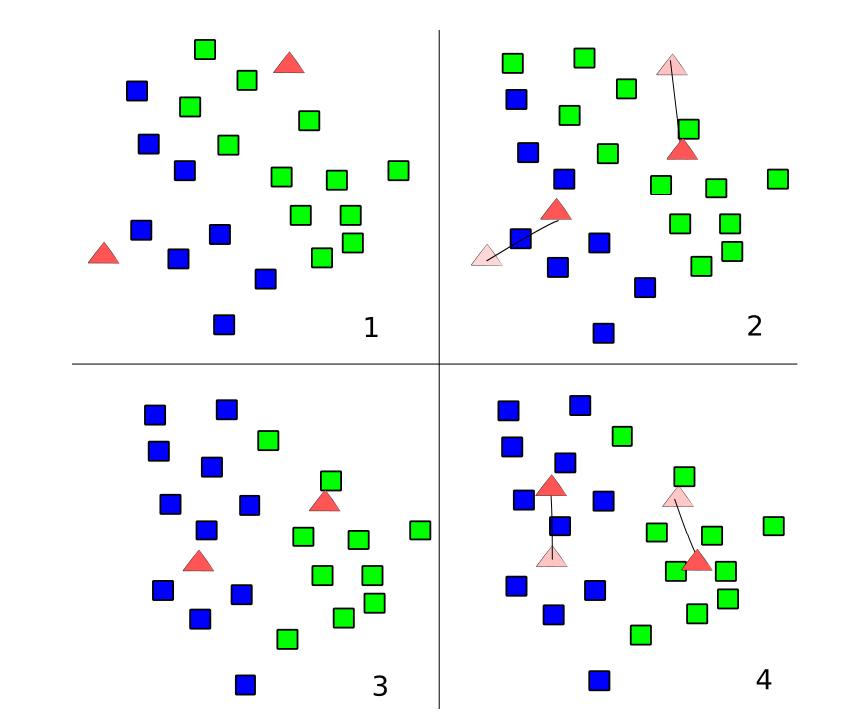
1))对于未分类的样本,首先随机以k个元素做为起始质心.为了简洁,也可以简化该算法,取元素列表中的前k个元素做为质心.

2))计算每个样本跟质心的距离,并将该样本分配非距离他最近质心所属的簇,重新计算分配好后的质心,质心开始向真正的质心移动.

3))在质心改变之后,他们的位移将引起各个距离的改变,因此需要重新分配各个样本

4)))在停止条件满足之前,不断重复第二步和第三步

可以使用不同类型的停止条件

我们可以选择一个比较大的迭代次数N,这样我们可能会遭遇一些冗余的计算,也可以选择N小一些,但是在这种情况下,如果本身质点不稳定,收敛过程慢,那么我们得到的结果就不能让人信服,这种停止条件也可以用作最后的手段,以防我们有一个非常漫长的迭代过程

另外还有一种停止条件,如果已经没有元素从一个雷转至另一个类,意味迭代的结束

(4)k均值的优缺点

扩展性很好(大部分的计算都可以并行计算)

应用范围广

缺点

需要先验证知识(需要预先知道可能的聚类数量)

异常值影响质心的结果

由于我们假设该图是凸的和各向同性的,所以对于非圆状的簇,该算法表现不是很好