神经网络让人觉得难以亲近的地方其实就是他的实现原理,至少远远没有原来我们接触到的各种基于统计的算法那么直观.我们原来在数据结构研究领域和基础算法研究领域说接触到的各种算法基本都是一些加减乘除,比大小,循环,分支,读写数据,用这些基本的组合就能够完成一个相对确定的目标任务,即便这个目标是一个比较复杂的算法内容.而神经网络和这种方式感觉上还真有那么一点不一样,我们先来看看 神经元是什么东西

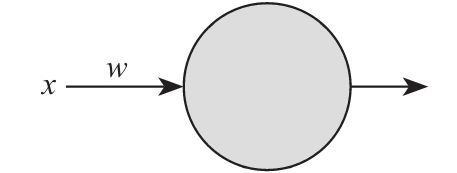
这就是一个最简单的神经元了,有一个输入,一个输出,所以它所表达的含义跟一个普通的函数没有什么区别.不过请注意,现在我们使用的神经元通常有两个部分组成,一个是”线性模型”,另一个是”激励函数”,如果你对机器学习不大了解的话,我们先说说这个”线性模型”

假设这个神经元函数表达为:

f(x)=x+1

那么这就是一个普通的一次函数,也就是说,当输入为1时,输出为2

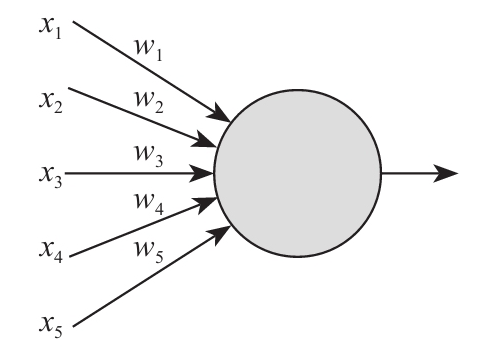
x既然可以是一个一维的向量,那其实也可以是5维的,当然也可以是100维或更多,我们就说它的输入为一个n维向量吧.按照前面一维向量的处理方式,我们可以建立一个有n个输入项的神经元f(x),把他展开写就是f(x1,x2…xn),咱们在这特别声明一下这个x是一个n维的向量,然后带有一个输出函数值output,这个output的输出值就是函数的输出值f(x),即output=f(x),而这个函数的处理我们写作:

f(x)=wx+b

这种方式也是神经元最核心部分对x所做的线性处理,其中x是一个1xn的矩阵,而w是一个nx1的权重矩阵,b是偏置项.

假设,n=5,那么x是一个1×5的输入矩阵,例如:

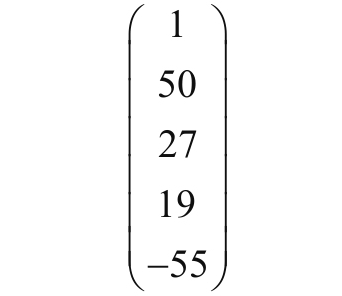
这个就是一个完整的特征向量x了,他表示了对一个样本的描述,这个描述是个多纬度的描述,具体每个维度指代的含义在不同的场景下是对应有不同解释的.比如这个矩阵有可能表示的是一个样本客户的个人财务状态,分别表示:

下一个用户可能又是别的值,这样一个一个样本组合起来形成了一个很大的样本空间–注意,这些样本最终都会用来训练模型,我们先记住他们的作用,后面再来逐步讲解究竟是怎么个用法.

w是一个nx1的矩阵,他表示的是一个权重的概念,例如:

[0.3,0.8,1.5,1.2,0.5]

他们分别表示:

[性别权重,年龄权重,年收入权重,忠诚度权重,负债权重]

还有一个b,b是一个实数值,或者把他视作一个1×1的矩阵也无妨.当我们在此回顾刚刚说的这个函数f(x)=wx+b的时候,我们试着来解读一下这个函数的含义.

wx相乘是两个矩阵进行内积的操作,乘出来是一个实数,最后再加上b.以我们刚刚的例子来看,我们先假设在这个例子中b是0,会得到这样一个结果,即f(x)=wx+b就变成了:

f(x)=1×0.3+50×0.8+27×1.5+19×1.2+(-55)x0.5+0 = 44.7

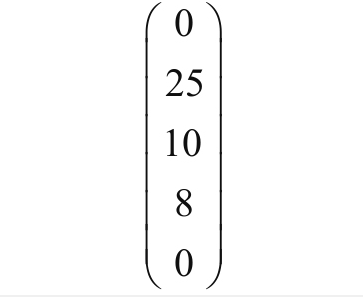
这个函数很有可能是某个金融机构用来评价客户质量所使用的评价函数,那么如果再有一个样本,譬如:

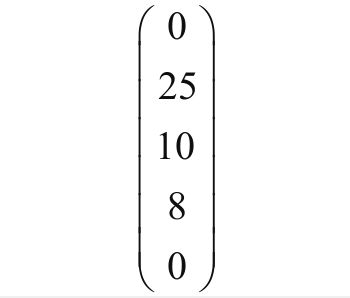
f(x)=0x0.3+25×0.8+10×1.5+8×1.2+0x0.5+0=51.6

在这样的一种评价体系下,第二位客户要比第一位客户获得更高的质量评分.

那么在这个金融机构的日常工作中就可以利用这个函数对客户的情况进行评分,并进行相应的信用额度给予,以及产品推荐等进一步的工作了.这就是一个神经元工作时最直观的感觉,w和x求内积,加b产生这样一个线性的结果输出.因为一个神经元也是一个逻辑简单的模型,所以它本身也能够单独胜任一些逻辑简单的场景.单个的神经元工作起来基本就是这个样子,只不过后面还会加一个激励函数而已.

那么,这个权重是谁规定的?

对机器学习有概念的朋友可能不会陌生,如果真的在某个金融机构里有这种公式,十有八九是通过”逆向”的方法得到的.就是收,我们先假设这里有一些未知的权重w,然后我们同时还拥有大量的客户样本,注意这个地方的样本可不是只有:

这种维度的标识,除此之外还有具体被赋予的分数–这个分数一定是由其他方式获得的,比如通过多年的业务经验总结,由业务专家给予每个样本所拥有的一个分数标签.这样依赖场景是怎么样的呢?

手里的数据:

分数1=性别1x性别权重+年龄1x年龄权重+年收入1x年收入权重+用户忠诚指数1x忠诚指数权重+负债1x负债权重+偏置

…

分数n=性别nx性别权重+年龄nx年龄权重+年收入nx年收入权重+用户忠诚指数nx忠诚指数权重+负债nx负债权重+偏置

我们提到过一个叫LOSS的函数:

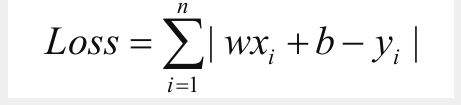
用来描述拟合与真实观测的差异之和,我们称之为残差,在这个例子中,如果想要得到比较合适的w和b,那就还是要想办法让这个函数LOSS(w,b)尽可能小,然后取满足这个状态的w和b