在本例中,我们会处理超过一个变量的问题
该数据包含1993个样本,采集的是波士顿郊区的房价,每个样本包括13个变量和该地区的平均低价.
我们用的样本跟原始样本唯一不一样的地方是去除了一个变量b,这个变量是按照种族化描述不同的郊区.
除此之外,我们将会选择对我们有用的变量,来建模线性方程.
1.有用的库和方法
本部分,我们会介绍一些有用的库和方法.这些库和方法不属于TensorFlow,我们将在本例以及本书的后续例子中使用,这对我们解决不同的问题非常有用.
2.pandsa库
当我们想快速读取常规大小的数据文件的时候,创建读缓存区和其他的机制可能会造成额外的开支,这是我们现实生活中常见的问题,pandsa库可以来处理这种问题.
Pandas官网(pandas.pydara.org)这样介绍Pandas:
“Pandas是一款开源的,基于BSD协议的Python库,能够提供高性能、易用的数据结构和数据分析工具。”它具有以下特点:
●能够从CSV文件、文本文件、MS Excel、SQL数据库,甚至是用于科学用途的HDF5格式。
●CSV文件加载能够自动识别列头,支持列的直接寻址。
●数据结构自动转换为NumPy的多维阵列。
3.数据集描述
数据集由CSV文件存储,我们用Panda库打开。本数据集包含以下变量。
●CRIM:城镇人均犯罪率。
●ZN:住宅用地超过 25000 sq.ft.的比例。
●INDUS:城镇非零售商用土地的比例。
●CHAS:Charles河空变量(如果边界是河流,则为1;否则为0)。
●NOX:一氧化氮浓度。
●RM:住宅平均房间数。
●AGE:1940 年之前建成的自用房屋比例。
●DIS:到波士顿5个中心区域的加权距离。
●RAD:辐射性公路的靠近指数。
●TAX:每 10000 美元的全值财产税率。
●PTRATIO:城镇师生比例。
●LSTAT:人口中地位低下者的比例。
●MEDV:自住房的平均房价,以千美元计。
我们可以通过以下的简单代码读取数据,并查看详细数据:
import pandas as pd
df = pd.read_csv(“./boston.csv”, header=0)
print(df.describe())
CRIM ZN INDUS CHAS NOX RM \
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean 3.613524 11.363636 11.136779 0.069170 0.554695 6.284634
std 8.601545 23.322453 6.860353 0.253994 0.115878 0.702617
min 0.006320 0.000000 0.460000 0.000000 0.385000 3.561000
25% 0.082045 0.000000 5.190000 0.000000 0.449000 5.885500
50% 0.256510 0.000000 9.690000 0.000000 0.538000 6.208500
75% 3.677082 12.500000 18.100000 0.000000 0.624000 6.623500
max 88.976200 100.000000 27.740000 1.000000 0.871000 8.780000
AGE DIS RAD TAX PTRATIO LSTAT \
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean 68.574901 3.795043 9.549407 408.237154 18.455534 12.653063
std 28.148861 2.105710 8.707259 168.537116 2.164946 7.141062
min 2.900000 1.129600 1.000000 187.000000 12.600000 1.730000
25% 45.025000 2.100175 4.000000 279.000000 17.400000 6.950000
50% 77.500000 3.207450 5.000000 330.000000 19.050000 11.360000
75% 94.075000 5.188425 24.000000 666.000000 20.200000 16.955000
max 100.000000 12.126500 24.000000 711.000000 22.000000 37.970000
MEDV
count 506.000000
mean 22.532806
std 9.197104
min 5.000000
25% 17.025000
50% 21.200000
75% 25.000000
max 50.000000
4.模型结构
本例模型虽然简单,但是它包含我们处理更复杂模型的所有元素
我们能够看到,解决机器学习问题的不同模块:模型,损失函数和梯度.TensorFlow有一个非常有用的功能,就是能够自动对模型的方程求导.
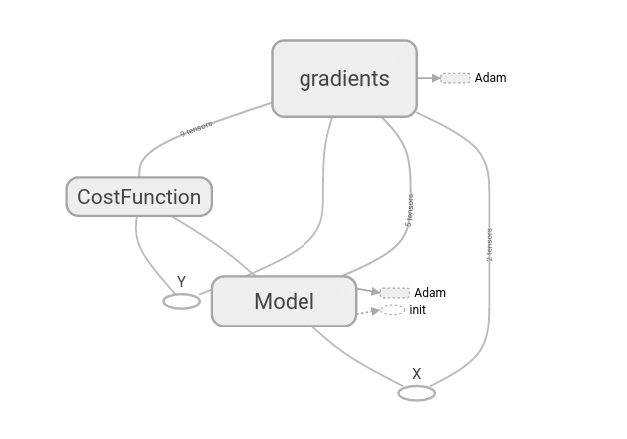
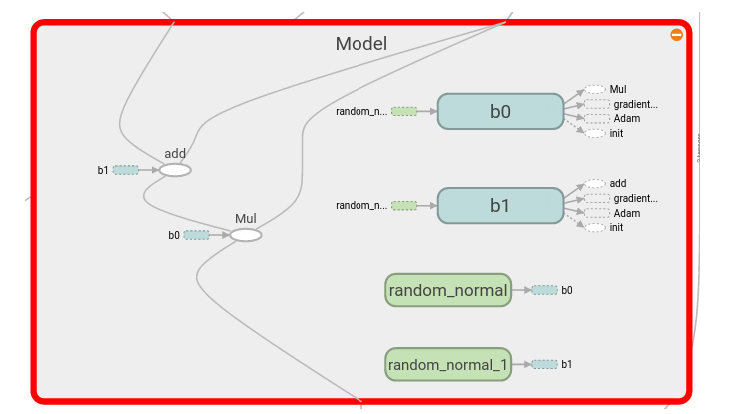
此处,我们可以找到之前部分w、b的定义和模型线性方程
X = tf.placeholder(“float”, name=”X”)
Y = tf.placeholder(“float”, name = “Y”)
with tf.name_scope(“Model”):
w = tf.Variable(tf.random_normal([2], stddev=0.01), name=”b0″) # create a shared variable
b = tf.Variable(tf.random_normal([2], stddev=0.01), name=”b1″) # create a shared variable
def model(X, w, b):
return tf.mul(X, w) + b # We just define the line as X*w + b0
y_model = model(X, w, b)
5.损失函数和Optimizer
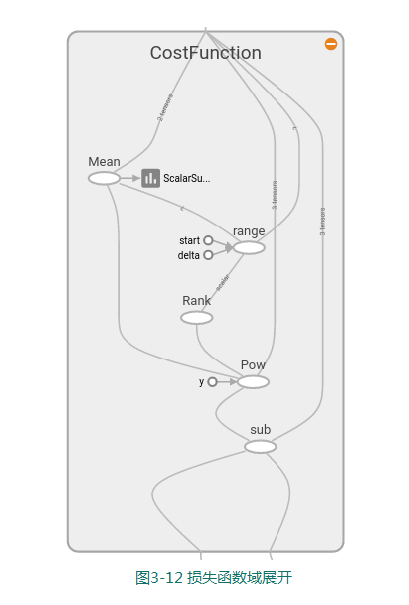
在本例中,我们使用最常见的均方误差作为损失函数,跟上例不同的是,这次是多变量;因此我们使用reduce_mean函数,来平衡多个纬度的误差值.其在tensorboard中的结构,如图所示:
with tf.name_scope(“CostFunction”):
cost = tf.reduce_mean(tf.pow(Y-y_model, 2)) # use sqr error for cost function
train_op = tf.train.AdamOptimizer(0.001).minimize(cost)
for a in range (1,50):
cost1=0.0
for i, j in zip(xvalues, yvalues):
sess.run(train_op, feed_dict={X: i, Y: j})
cost1+=sess.run(cost, feed_dict={X: i, Y: i})/506.00
#writer.add_summary(summary_str, i)
xvalues, yvalues = shuffle (xvalues, yvalues)
print (cost1)
b0temp=b.eval(session=sess)
b1temp=w.eval(session=sess)
print (b0temp)
print (b1temp)
6.停止条件
本例的停止条件比较简单,只要等待所有样本执行完特定的次数,就可以结束训练.