下一步就是选择一个办法最小化损失函数.在微积分中,我们学过,想要获得局部最小值,可以对参数求偏导,并让偏导等于0.这个方法有两个要求,第一是偏导存在,第二最好是凸函数.可以证明最小方差函数满足这两个条件.这对避免局部最小值的问题,非常有帮助.最小方差损失函数如图所示:

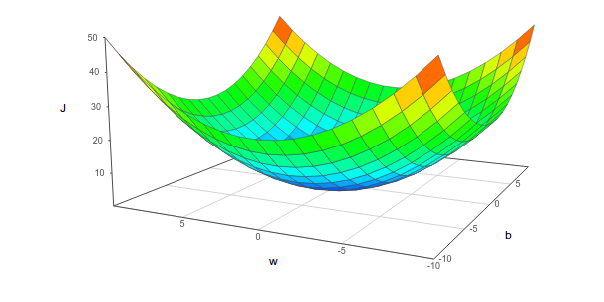
1.最小方差的全距最小值

我们通过矩阵的形式来计算最小方差的解:

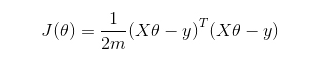
此处,J是损失函数,参数的解如下:

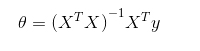
2.迭代方法:梯度下降

梯度下降方法是在机器学习领域使用的最多的优化方法.该方法沿着梯度的反方向,寻找损失函数的局部最小值.

对于二维的线性回归,我们先随机定义一个权值θ,做为线性方程的系数,然后使用如下方程,循环迭代更新θ的值

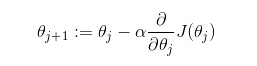
该式子的机制很简单,我们从一个初始值开始,沿着方程改变最大方向的反方向移动.α被称作步长(step),会影响每次迭代移动的大小.

最后一步是跳出迭代的测试.以下两种情况满足其中之一就跳出循环:两次迭代之间的差值大于一个epsilon或者迭代次数达到阈值.

如果方程是非凸的,建议多找几个初始值运用梯度下降法,最后选择损失函数最低的那个参数作为结果.因为,非凸函数的最小值,可能是局部最小值,最终的结果依赖于初始值.所以推荐选多个初始值.

3.TensorFlow中的优化方法–训练模块

训练或者参数优化是机器学习工作流中重要的组成部分

在TensorFlow中有一个tf.train模块专门来解决这个问题,在该模块中,集成了很多种数据科学家常用的优化策略.这个模块提供的主要对象被称作Optimizer(优化器).

4.tf.train.Optimizer类

优化器(Optimizer)类用来计算损失函数的梯度,并将他们应用于同一模型的不同变量.我们最常用的优化方法有梯度下降(radient descent),adam,adagrad.

要注意,Optimizer这个类本身不能被初始化,只能初始化它的子类.

正如我们之前所讨论的,TensorFlow可以通过符号语言定义函数,所以梯度也可以通过符号语言的方式使用,这能够提高结果的准确性并丰富对数据的操作.

使用Optimizer类,我们要遵循以下步骤:

(1)为需要优化的参数,创建一个Optimizer

opt = GradientDescentOptimizer(learning_rate= [learning rate])

(2)创建一个操作,调用minimize方法,最小化损失函数

optimization_op = opt.minimize(cost, var_list=[variables list])

minimize函数要遵循以下的格式：

tf.train.Optimizer.minimize(loss, global_step=None, var_list=None,gate_gradients=1, aggregation_method=None,colocate_gradients_with_ops=False, name=None)

主要的参数如下。

●loss：存放损失函数每轮迭代后的数值。

●global_step：Optimizer执行一次迭代，加一。

●var_list：需要优化的变量。

事实上,optimizer方法内部调用了compute_gradients和apply_gradients两个方法,如果你想在使用梯度之前,对梯度进行额外的处理,可以先使用compute_gradients方法计算出梯度,然后调用apply_gradients方法.如果我们想只使用一步来训练,我们一定需要按照opt_op.run()的方式去执行run方法

5.其他Optimizer实例类型

以下是其他Optimizer实例类型

●tf.train.AdagradOptimizer：自适应梯度Optimizer，学习率随着时间递减；

●tf.train.AdadeltaOptimizer：增强版Adagrad，学习率不再绝对随着时间衰减；

●tf.train.MomentumOptimizer：实现Momentum优化算法；

●TensorFlow还实现了其他的Optimizer，如tf.train.AdamOptimizer,tf.train.FtrlOptimizer, tf.train.RMSPropOptimizer。